معادلات لقياس المساحة

مساحة الدائرة ذات الشعاع r.

مساحة المستطيل: الطول × العرض

مسلمة مساحة المستطيل والتي تنص على أن مساحة المستطيل تساوى طوله×عرضه وهذا شيء بديهى يمكن إدراكه بدون البرهنة عليه وذلك بملاحظة أنه عند فرض مستطيل عرضه الوحدة (لكى يكون عرضه غير مؤثر في المساحة بحيث يكون الطول وحده هو الذي يتحكم في قيمة المساحة) وطوله عدد معين من الوحدات نلاحظ أن عدد الوحدات المربعة والتي تشكل مساحة المستطيل يساوى عدد الوحدات الطولية التي تشكل طول المستطيل وبزيادة عدد وحدات الطول نلاحظ أن مساحة المستطيل تزداد بنفس المقدار ومن ذلك يتضح أن مساحة المستطيل تساوى طوله×عرضه.

مساحة المثلث: ½ × القاعدة × الارتفاع $S = 1/2 bh$
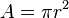
مساحة الدائرة: $A = \pi r^2 \,$
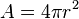
مساحة سطح الكرة: $A = 4 \pi r^2 \,$
مساحة الشكل البيضاوي (أو الأهليجي): باي( ${\pi}$ ) × نق المحور الأكبر × نق المحور الأصغر
يمكن قياس مساحة الأشكال المعقدة والمساحات المحصورة بين الدوال باستخدام علم التفاضل
مساحة المربع: طول الضلع تربيع (ل²)

وحدات قياس المساحة

سنتيمتر مربع سم²
المتر مربع اختصاره م² ، وهي وحدة مشتقة من المتر (وحدة قياس دولية)
هكتار يساوي 10 000 متر مربع
كيلومتر مربع اختصاره كم² يساوي 1 000 000 (مليون) متر مربع
قدم مربع ويساوي 0.09290304 متر مربع
ياردة مربعة وتساوي 9 أقدام مربعة أي 0.83612736 متر مربع
ميل مربع ويساوي 2.5899881103 كيلومتر مربع
الفدان ويساوي 4200.83 متر مربع، وينقسم إلى 24 قيراط وكل قيراط 24 سهم حيث مساحة القيراط 175.09 متر مربع ومساحة السهم 7.29 متر مربع.

والفدان أكبر قليلا من الإيكر الأنجلو أمريكي.

الإيكر (Acre) يساوي 4046.8564224 متر مربع.
قصبة (وحدة تستخدم في البلاد العربية) تعادل 30،25 ياردة مربعة.

مساحة بعض الأشكال الهندسية

يعطي هذا الجدول معادلات المساحة لبعض الأشكال في الهندسة المستوية :

الشكل	صفـاته	المساحة $A$
المربع	طول الضلع $a$	$A = a^2$
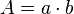المستطيل	الطول والعرض $a,\,b$	$A = a \cdot b$
المثلث (انظر أيضا: مساحة المثلث)	القاعدة $g$ ، الارتفاع $h$ ، عمودي على $g$	$A = \frac{g \cdot h}{2}$
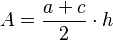شبه منحرف	الضلعان المتوازيان $a,\,c$ ، الارتفاع $h$ ، عمودي على $a$ و $c$	$A = \frac{a + c}{2} \cdot h$
المعين	المحورين $d_1$ و $d_2$	$A = \frac{d_1 \cdot d_2}{2}$
متوازي الأضلاع	طول الضلع $a$ ، الارتفاع $h_a$ ، عمودي على $a$	$A = a \cdot h_a$
دائرة	نصف القطر $r$	$A = \pi r^2$
قطع ناقص	المحور الطويل $2a$ والمحور القصير $2b$	$A = \pi ab$
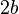مسدس منتظم	طول الضلع $a$	$A = \frac{3\sqrt{3}}{2} a^2$

من أجل تعيين مساحة متعدد الأضلاع فيمكن تقسيمه إلى مثلثات، ثم جمعها بعد حساب مساحاتها. وإذا كانت الإحداثيات $(x_i, y_i), i=1 \dots n$ لعدد $n$ من الأركان لمتعدد الأضلاع معروفة، فيمكن حساب المساحة بواسطة معادلة جاوس لشبه المنحرف:

$A = \frac{1}{2} \sum_{i=1}^n (y_i + y_{i+1})(x_i-x_{i+1})$

حيث:

$x_{n+j}=x_j$

و $y_{n+j}=y_j$

الأشكال أخرى يمكن تقريبها لمضلع متعدد الأضلاع وتكملة حسابها بالتقريب.

حساب مساحة اسطح بعض الأجسام

رباعي السطوح Tetraeder

Gerader Kegel mit abgewickelter Mantelfläche

الشكل	صفاتـه	Oberfläche $A$
مكعب	Seitenlänge $a$	$A = 6a^2$
متوازي أضلاع	الطول، والعرض، والارتفاع $a,\,b,\,c$	$A = 2(ab+ac+bc)$
رباعي السطوح	طول الضلع $a$	$A = \sqrt{3}\,a^2$
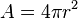الكرة (انظر أيضا: سطح الكرة)	نصف القطر $r$	$A = 4\pi r^2$
أسطوانة	نصف قطر القاعدة $r$ ، الارتفاع $h$	$A = 2 \pi r (r + h)$
مخروط	نصف قطر القاعدة $r$ ، الارتفاع $h$	$A = \pi r (r + \sqrt{r^2+h^2})$
طارة (رياضيات)	نصف قطر الطارة $R$ , نصف قطر المقطع $r$	$A = 4\pi^2 \cdot R \cdot r$

حساب التكامل

تعيين المساحة تحت منحنى بين النقطتين a وb بالتقريب عن طريق تقسيمها إلى مستطيلات ضيقة. وهذه هي فكرة حساب التكامل.

يستعمل حساب التكامل بغرض تعيين المساحة تحت منحنى في منحنى بياني. وتنبع تلك الفكرة من امكانية تقسيم المساحة المحصورة بين المنحنى البياني والمحور الأفقي $x$ إلى مجموعة من المستطيلات الضيقة، وينبع معنى حساب التكامل من جعل عرض المستطيلات المختارة يقترب من الصفر (عندما تقترب dx من الصفر).

Slideshow